UTXO uh-oh…

I’m adding entries to my list of objections to raising the maximum block size as I run across them in discussions on reddit, in IRC, etc.

This is the technical objection that I’m most worried about:

More transactions means more memory for the UTXO database

I wasn’t worried about it yesterday, because I hadn’t looked at the trends. I am worried about it today.

But let me back up and explain briefly what the UTXO database is. UTXO is geek-speak for “unspent transaction output.” Unspent transaction outputs are important because fully validating nodes use them to figure out whether or not transactions are valid– all inputs to a transaction must be in the UTXO database for it to be valid. If an input is not in the UTXO database, then either the transaction is trying to double-spend some bitcoins that were already spent or the transaction is trying to spend bitcoins that don’t exist.

Jameson Lopp’s statoshi.info web site keeps track of the size of the UTXO database over time. Over the last 11 months it looks like this:

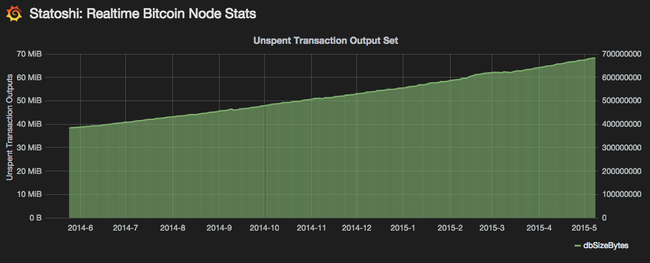
So the UTXO size has doubled in the last year. That would be OK if the price of memory was halving every year, but memory prices dropped only about 20% last year. Even assuming Moore’s Law kicks in again as new memory chip technologies roll out we would still have the UTXO set growth outpacing the advance of technology.

Today, the UTXO database is about 650MiB on disk, 4GB when decompressed into memory. DRAM costs about $10 per GB, so you need to spend about $40 on memory if you want absolute fastest access to the UTXO. Not a big deal.

Assuming the UTXO set continues to double and RAM prices continue to drop 20% per year, next year you’ll have to spend about $64. Ten years from now, over $4,000…

… except the maximum block size will stop the exponential growth. A one megabyte block is room for about 100 million 500-byte transactions per year. If every one of them increased the UTXO set by 500 bytes, that would grow the UTXO set 50 gigabytes a year. So very worst case running a full node with the entire UTXO set in RAM is $500 per year, at today’s DRAM prices. That cost would decline as memory prices fell.

Allowing more transactions with no other changes would very likely accelerate the UTXO set growth, making it more expensive, more quickly, to run a fully validating node. And worst case would be twenty times as expensive; $10,000 per year. Affordable for a business, not for an individual.

That is a very good reason to oppose increasing the maximum block size.

But is the worst case realistic? The entire UTXO set doesn’t have to be in RAM; it can be stored on an SSD or spinning hard disk. The access pattern to the UTXO is not random; outputs that were spent recently are more likely to be re-spent than outputs that have not been spent in a long time. Bitcoin Core already has a multi-level UTXO cache, thanks to the hard work of Pieter Wuille.

Solid-state-disk (SSD) prices are about $0.50 per GB, spinning disks are about $0.05 per GB. Worst case UTXO storage for 20MB blocks is about one terabyte per year, or $500 per year at today’s SSD prices. $50 per year at today’s hard disk prices.

That’s not so bad!

But there is a tradeoff – if you don’t store the entire UTXO set in DRAM, then it will take you longer to validate blocks. How much longer depends on how much memory you’re dedicating to the UTXO cache, the speed of your SSD or hard drive, and how well a new block’s transactions match typical transaction patterns.

Unless you are mining, taking longer to validate new blocks isn’t a problem as long as you can validate them fast enough to keep up with the 10-minute-average block time.

If you are mining, then taking longer to validate new blocks puts you at a disadvantage, because you can’t (or, at least, shouldn’t) start mining on the new best chain until you’ve fully validated the new block. I’ll write about that more when I respond to the “Bigger blocks give bigger miners an economic advantage” objection.